zuubaDigital

Paths

The path element

The path element is used to create complex shapes and curves. It is the most powerful shape element, and can be used to create any other shape element.

the d attribute

The “d” attribute contains all the path commands that define the path.

<path d="M 397,319 c 0,177 -80,316 -178,319 C 90,643 -78,515 40,319 131,168 120,0 219,0 c 98,0 178,143 178,319 Z" fill="#EDE9E9"/>

M or m - moveTo

The “M” command stands for moveto, and is used designate the starting point of the path.

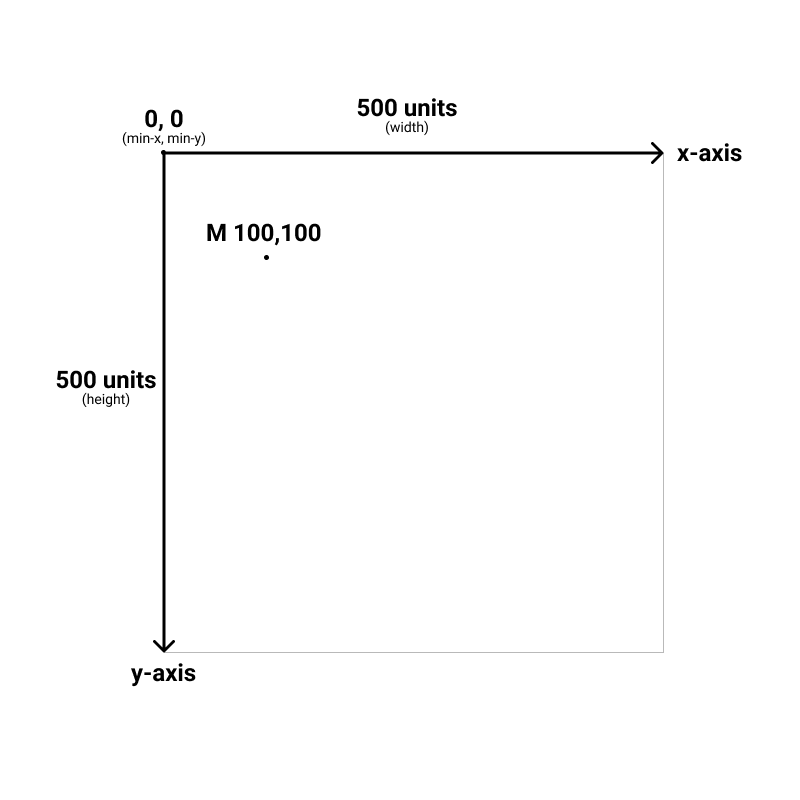
<path d="M 100,100" />

In the example below, the starting point is 100,100. The M is always the first command. It can also be used throughout the path, wherever you wish to “pick up” your pen and start drawing the path from a different location.

L or l - lineTo

This command draws a line from the previous point to the designated coordinate

In the example below, we can draw to the absolute point of L 400,100, or we can use a relative path with l 300, 0 (300 to the right and 0 down). We get the same result either way.

L - draws a line to the absolute coordinate that follows the command.
l - draws a line to the relative coordinate that follows the command.

1
2

<path 
d="M 100,100 L400,100" />

absolute path

1
2

<path 
d="M 100,100 l300,0" />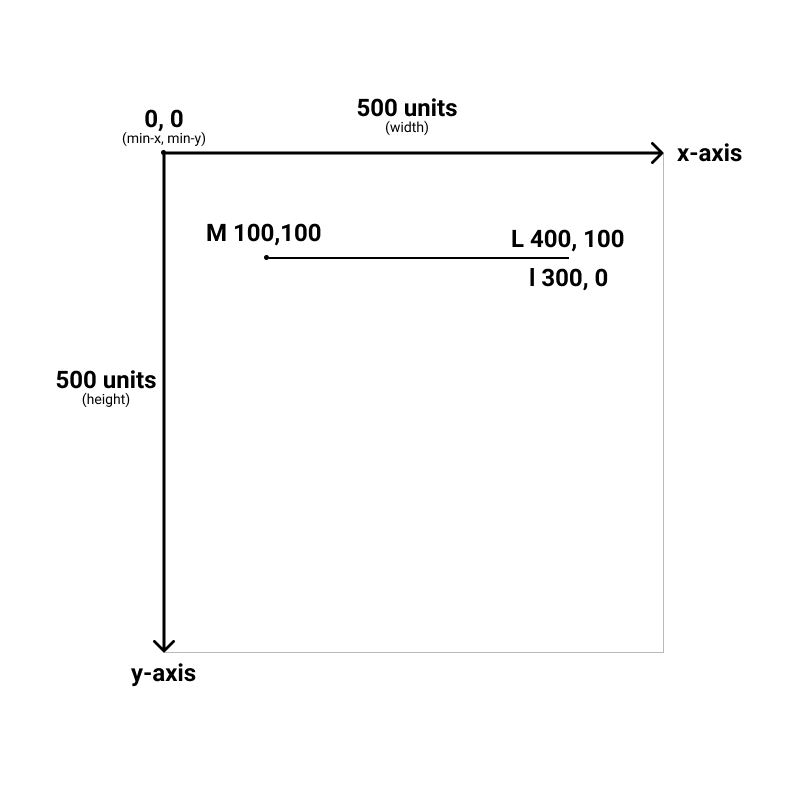

relative path

V or v - vertical line

Draws a vertical line to the designated y position.

In the example below we're drawing a vertical line to the absolute y position of 400 or the relative y position of 300 (300 down from the previous point)

V - draws a line to an absolute y position.
v - draws a line to an relative y position.

1
2

<path 
d="... L400,100 V400" />

absolute path

1
2

<path 
d="... L400,100 v300" />

absolute path

H or h - horizontal line

Draws a horizontal line to the designated x position.

In the example below we're drawing a horizontal line to the absolute x position of 100 or the relative x position of -300 (300 to the left of the previous point)

H - draws a line to an absolute x position.
h - draws a line to an relative x position.

1
2

<path 
d="...  V400 H100" />

absolute path

1
2

<path 
d="... v300 h-300" />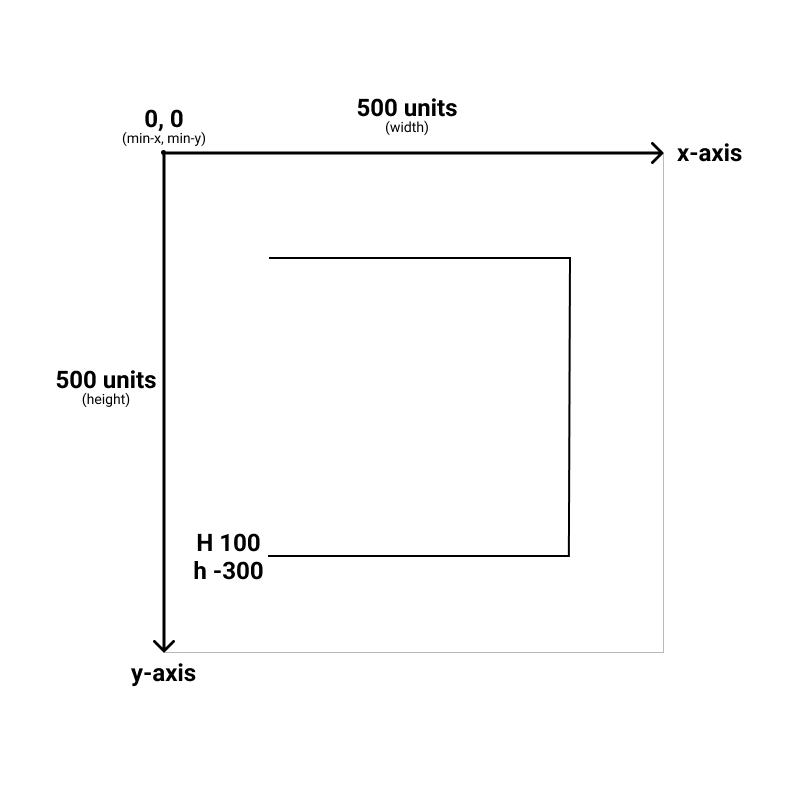

absolute path

Z or z - close path

The z command draws a line from the “current” point to the start point, closing the path.

Z or z - closes the path

1
2

<path 
d="...  H100 Z" />

1
2

<path 
d="...  h-300 z" />

Bezier curves

The bezier curve commands allow you to create smooth curves from a start point, an end point, and one or two control points.

The actual bezier curve math is beyond the scope of this course, but you can think of the control point as exerting a gravitational force that bends the line.

Q or q - Quadratic Bezier curve

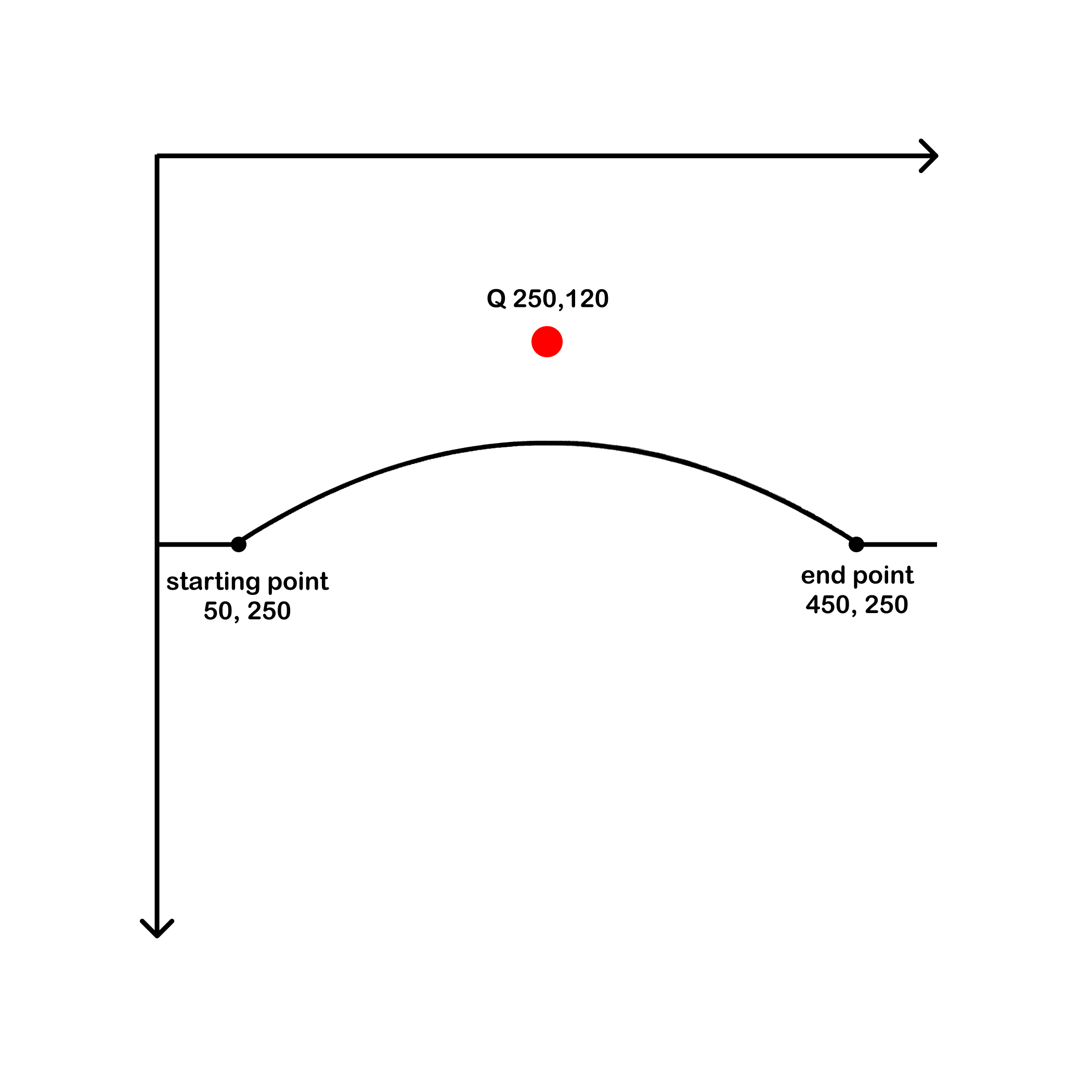
paths_bezier_

Above is an example of a Quadratic Bezier curve, where a start point, an end point, and a single control point is used to bend the line.

The start point is the coordinate before the Q (50, 250). The value pair after the Q (250, 120) is the control point. The capital Q signifies that the point is an absolute coordinate. The end point is the point that follows the control point (450,250)

<path 
d="M 0,250 L 50,250 Q 250,120 450,250 L 500,250"
stroke="black" 
fill="none"/>

Here's the same line using the lower case q, which uses relative positioning. With relative positioning the control point (200, -130) and the end point (400, 0) are described in terms of their distance (dx, dy) from the start point of the curve (50, 250). So the control point is 200 units to the right and -120 units up from the start point, and the end point is 400 units to the right and 0 units up from the start point.

<path 
d="M 0,250 L 50,250 q 200,-130 400,0 L 500,250" 
stroke="black" 
fill="none"/>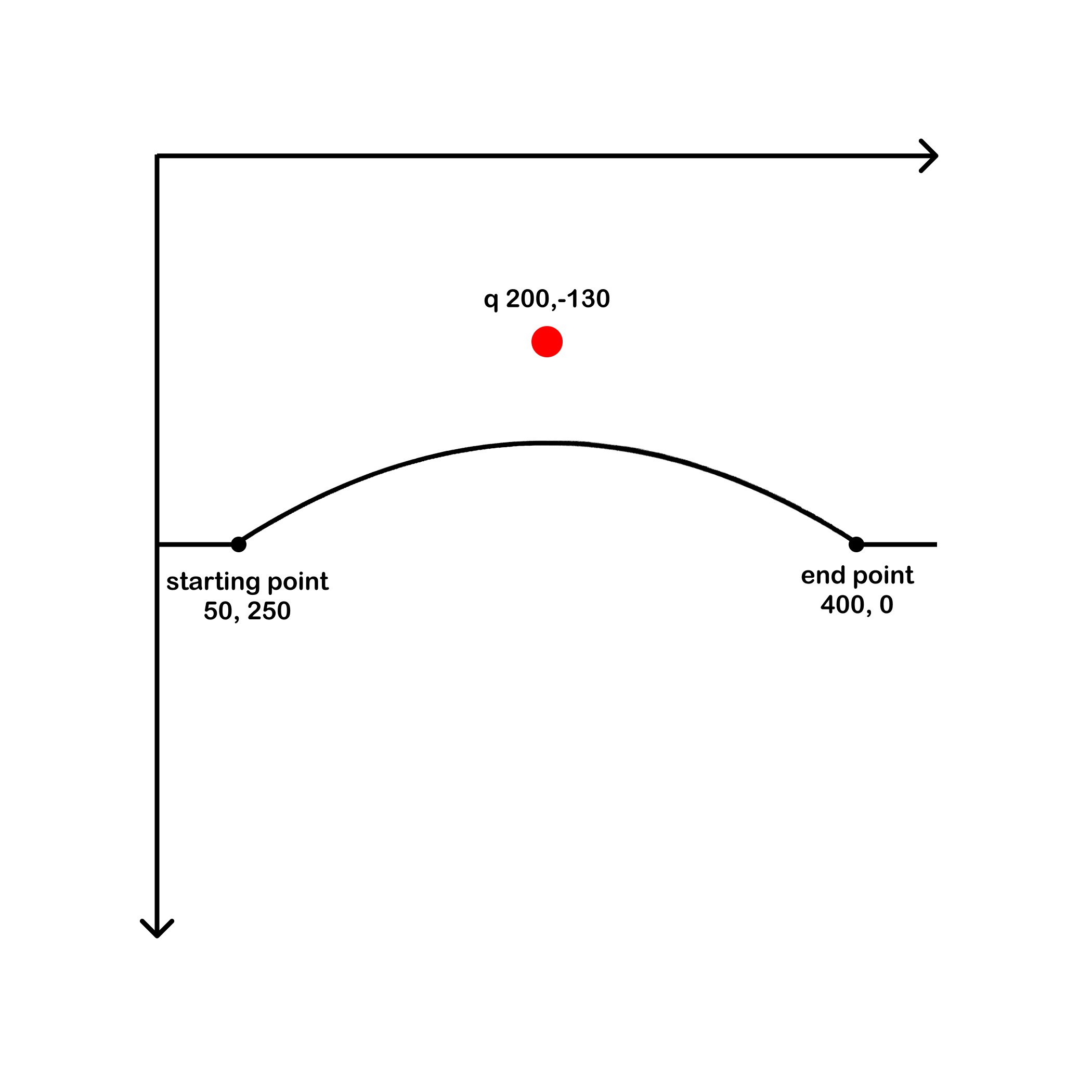

Interactive Demo - Quadratic Bezier

C or c - cubic bezier curves

Cubic bezier curves use two control points to bend a line. The coordinate right before the C (50, 250) represents the start point of the curve. The two points after the C (200,125 and 300,425) represent the absolute coordinates of the control points, which are followed by the end point (450, 250) of the curve. The capital C signifies that the control points are absolute coordinates.

<path 
d="M 0,250 L 50,250 C 200,125 300,425 450,250 L 500,250"
stroke="black" 
fill="none"/>

And here is the same line using the lower case c, which uses relative positioning from the start point (50, 250) for the two control points( dx:150, dy:-125 and dx:250, dy:175) and the end point (dx:400, dy:0)

<path 
d="M 0,250 L 50,250 c 150,-125 250,175 400,0 L 500,250"
stroke="black" 
fill="none"/>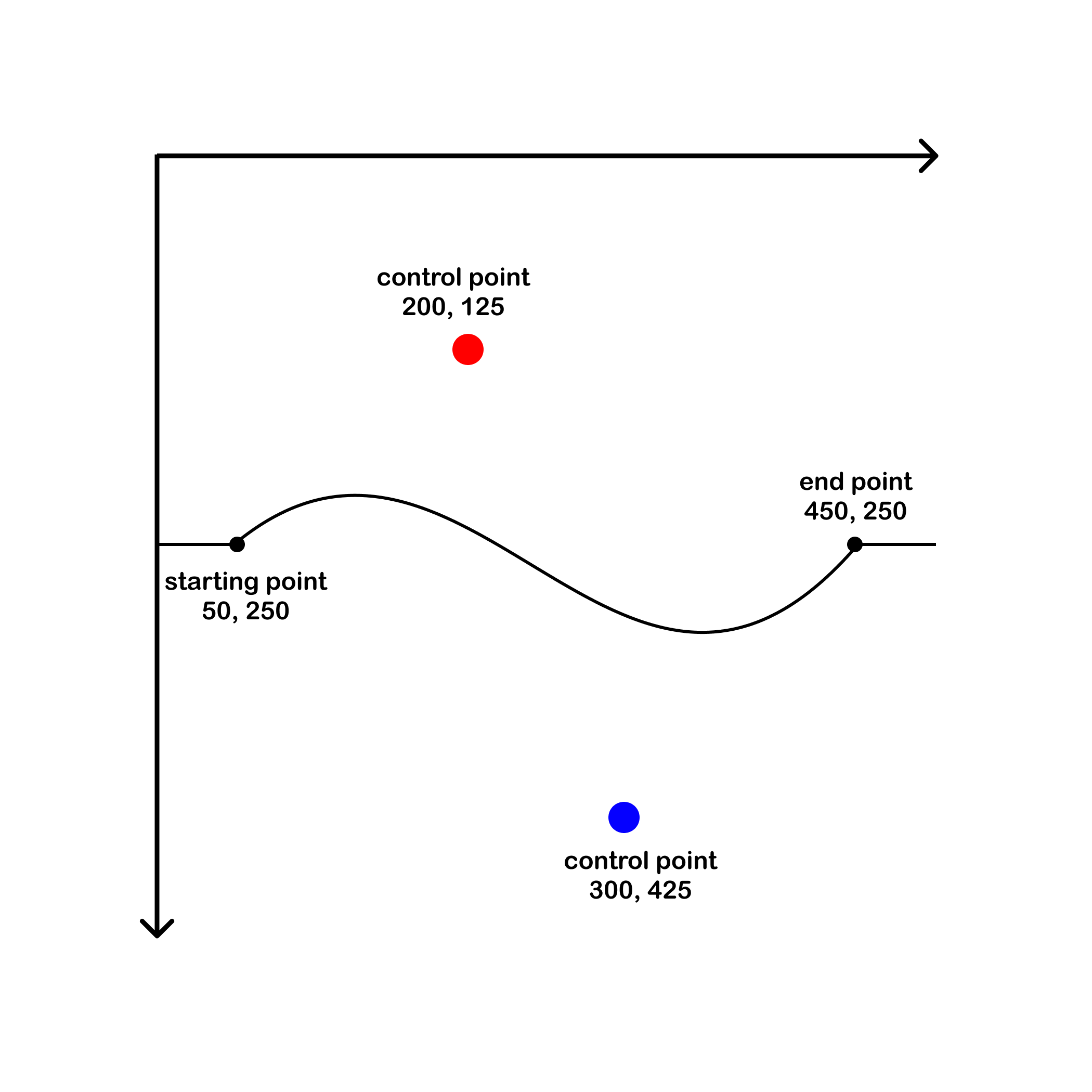

Interactive Demo - Cubic Bezier

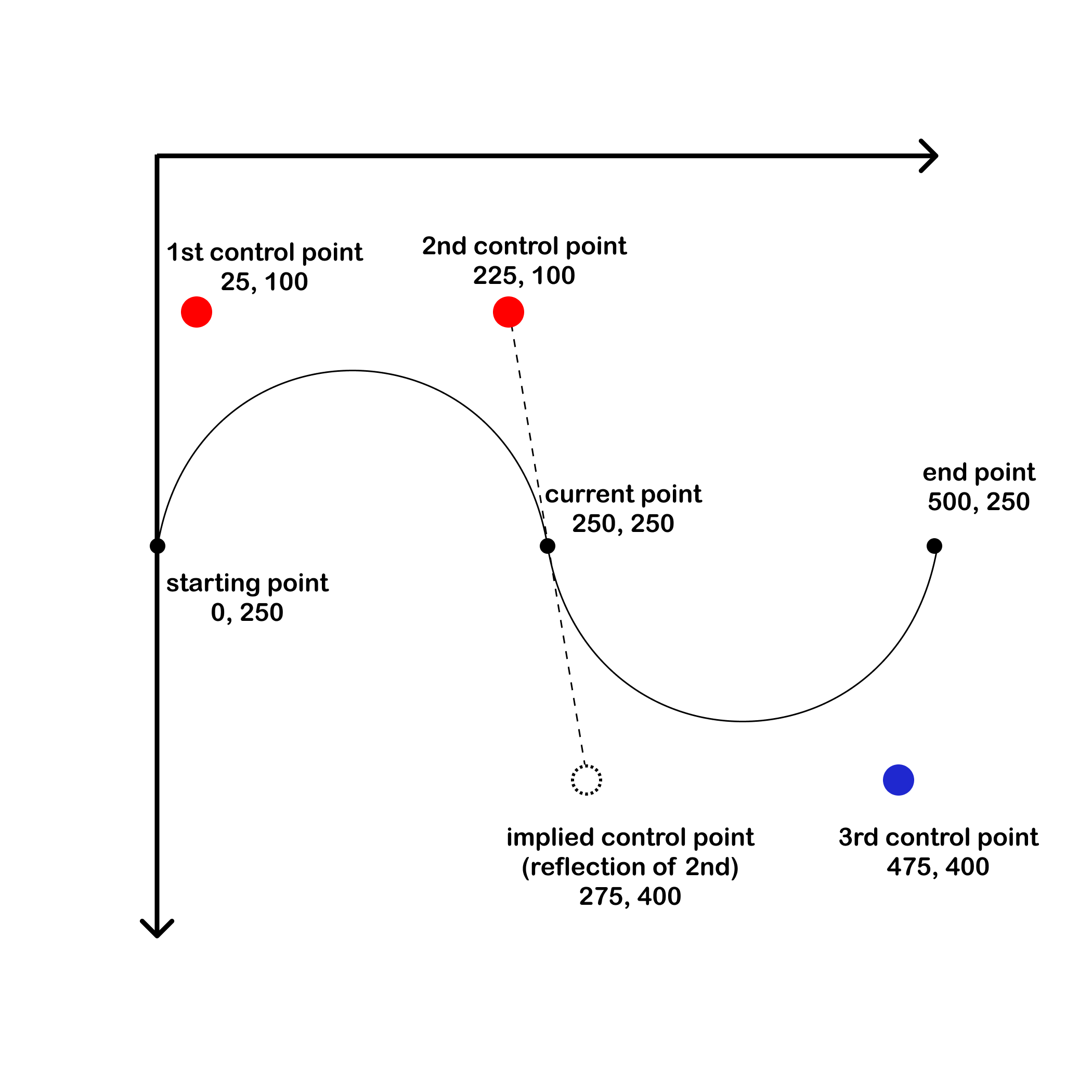
T or t - smooth quadratic curves

The smooth quadratic command (T or t) draws a quadratic curve from the current point (the point prior to the command - in the example below, 250,250) to the point after the command, using an implied control point that is the REFLECTION of the previous control point (125, 100). So an implied control point that is the reflection of the prior control point would be 375, 400.

control point - the point directly after the Q (125,100).
current point - the point after the control point and before the T (250,250).
T - creates an implied control point that is the reflection of the control point.

<path 
  d="M 0,250 Q 125,100 250,250 T 500,250" 
  stroke="black" 
  fill="none" />

Here's the same curve with the implied point written out:

<path 
  d="M 0,250 Q 125,100 250,250 Q 375,400 500,250" 
  stroke="black" 
  fill="none" />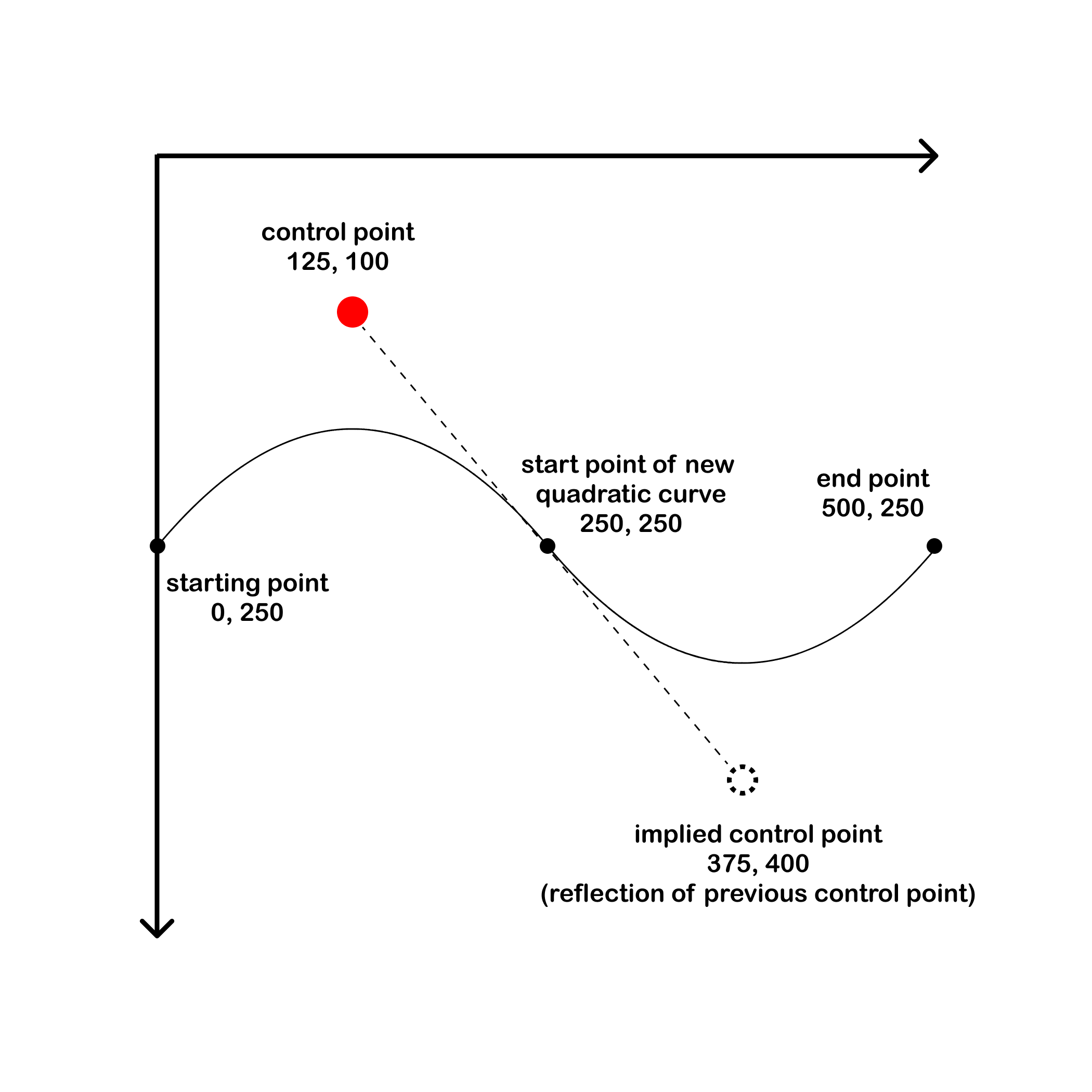

Interactive Demo - Smooth Quadratic

Smooth Cubic

The smooth cubic command (S or s) draws a cubic curve from the current point to the cubic control point after the command, assuming a cubic control point that is the reflection of the previous cubic control point.

cubic control point - current point - (implied point) - control point

<path 
  d="M 0,250 C 25,100 225,100 250,250 S 475,400 500,250" 
  stroke="black" 
  fill="none"/>

Interactive Demo - Smooth Cubic

< Prev: Basic Shape Elements Next: Text >